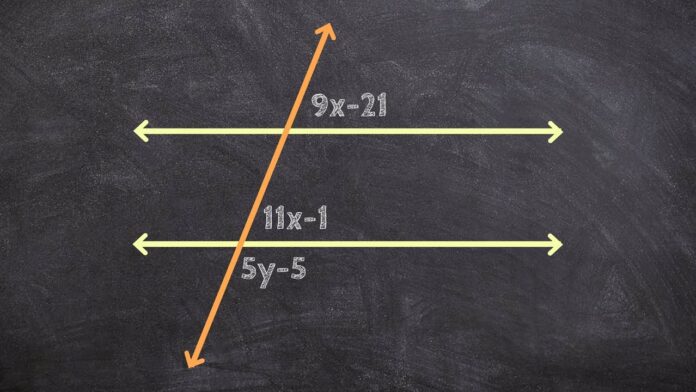
In geometry, lines are one of the fundamental concepts that researchers and mathematicians’ study extensively. You’ll often see diagrams with parallel lines and a transversal (a line that crosses them). When lines meet or cross each other in different ways, they form interesting shapes and angles. Learning how these lines and angles work together is key to understanding geometry better!
What are Parallel Lines?
Parallel lines are two straight lines that never meet, no matter how far they extend. They stay the same distance apart and run in the same direction.
Example:
Think of the two rails of a train track. No matter how far the track goes, the rails never touch. These rails are like parallel lines.
What is a Transversal?
A transversal is a line that cuts across two or more other lines. It can intersect parallel lines or lines that aren’t parallel.
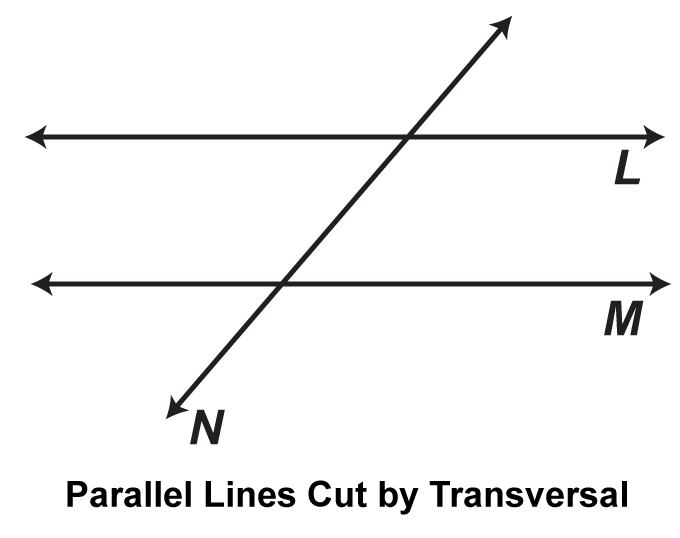
Diagram of Parallel Lines Cut by a Transversal
Here’s what you’ll often see:
- Two parallel lines (let’s call them L and M).
- A transversal line (let’s call it N) crossing both parallel lines.
Angles Created by a Transversal
When a transversal cuts parallel lines, it creates several angles at the points where the lines intersect. These angles have special relationships. Here are some key angle types:
Corresponding Angles
These angles are in the same relative position at each intersection. They are always equal when the lines are parallel.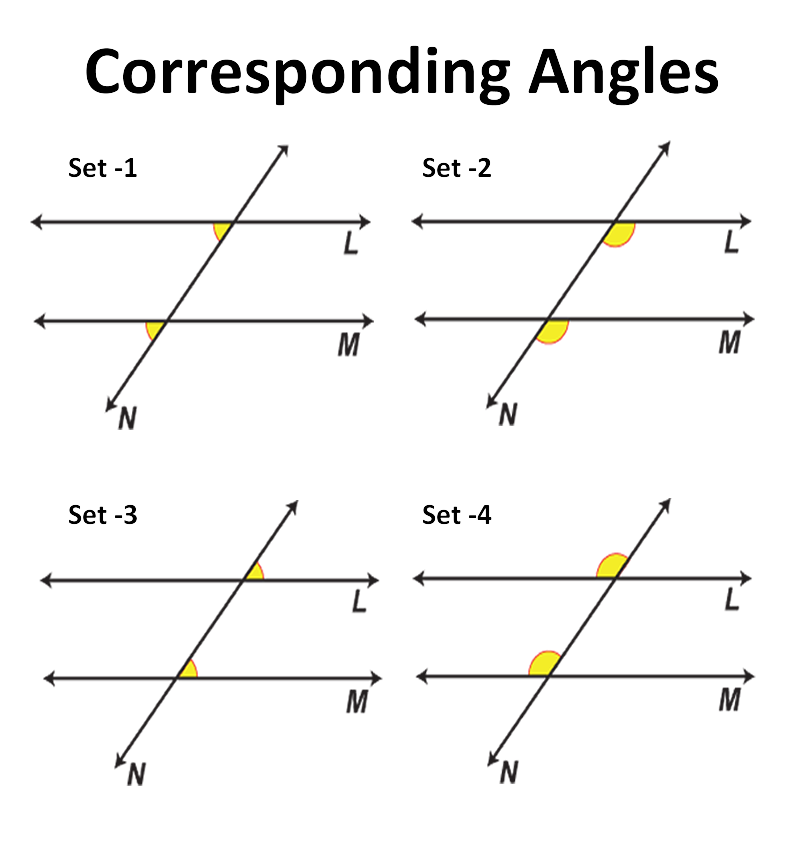
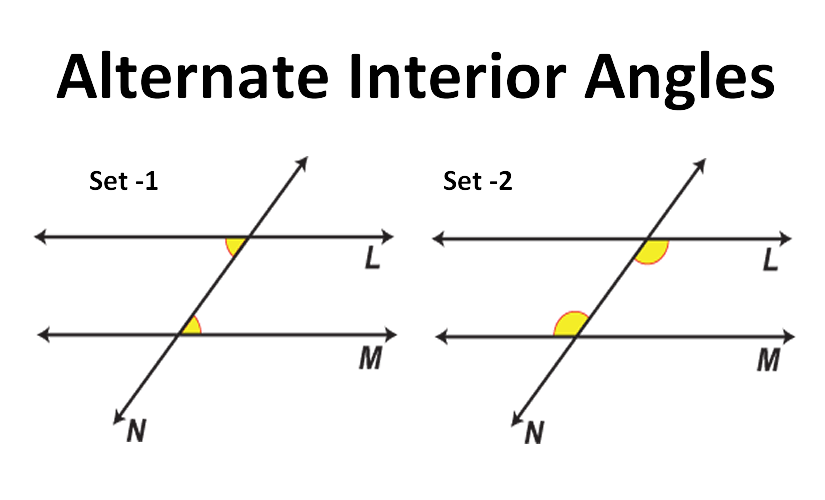
Alternate Interior Angles
These are inside the parallel lines and on opposite sides of the transversal. They are also equal.
Alternate Exterior Angles
These are outside the parallel lines and on opposite sides of the transversal. Like alternate interior angles, they are equal too.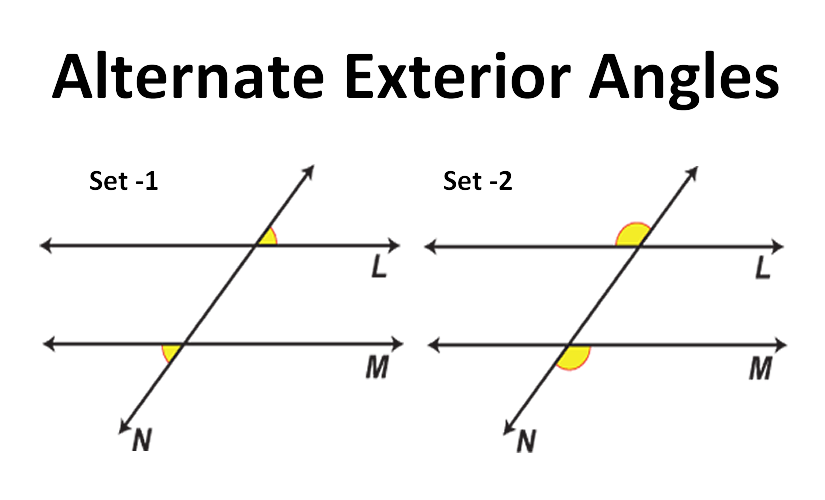
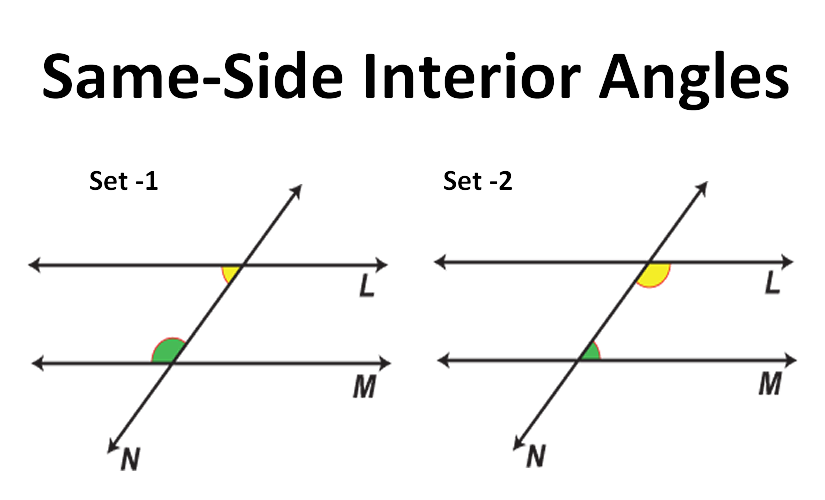
Consecutive Interior Angles (Same-Side Interior Angles)
These are on the same side of the transversal, inside the parallel lines. These angles add up to 180 degrees.
Quick Recap:
- Parallel Lines never meet.
- A Transversal cuts across two or more lines.
- When a transversal cuts parallel lines, it creates special angles (corresponding, alternate, consecutive).
- To confirm if lines are parallel, check for angle relationships!
Now that you understand the basics, you’ll easily recognize parallel lines cut by a transversal in any diagram! Geometry offers a fascinating world of shapes and formations, and the intersection of parallel lines and transversals is just one example of the intricacies it presents.